数学科学学微分方程团队周立群教授近日在IEEE Transactions on Network Science and Engineering发表了题为“Global Polynomial Stabilization of Impulsive Neural Networks With Bidirectional Proportional Delays”的学术论文。该研究首次提出了一种新的向量形式的时滞微分不等式方法，应用于解决双向比例时滞脉冲神经网络的全局多项式镇定问题。

脉冲神经网络的镇定在优化问题中有着广泛的应用。由于网络运行过程中放大器的开关和信号传输导致时滞不可避免。比例时滞是一类无界时变时滞，双向比例时滞可更好的刻画神经网络的时滞情况，但是比例时滞的无界性给神经网络镇定研究带来了很大的挑战。传统的构造Lyapunov泛函的方法不容易解决向量形式的双向比例时滞脉冲神经网络(BPDINNs)的镇定问题。为了克服这一困难，周立群教授及其研究团队通过设计易于硬件实现的反馈控制器，并利用M-矩阵的性质构造了一个新的向量形式的时滞微分不等式。利用提出的时滞微分不等式、M-锥和M-矩阵的性质以及矩阵谱半径理论，证明了闭环系统平衡点存在且是唯一。进而得到了所研究的BPDINNs的全局多项式镇定准则，易于验证。该方法的创新性和优点是没有使用通常的构造Lyapunov泛函的研究方法，为双向比例时滞脉冲神经网络的动力学研究提供了新的研究方法及思路。数值仿真如图1所示。

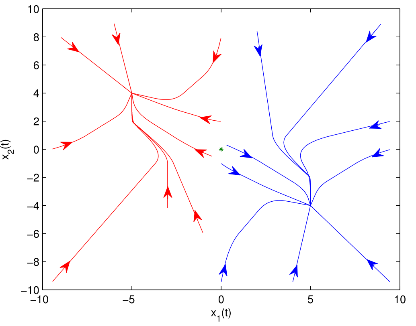
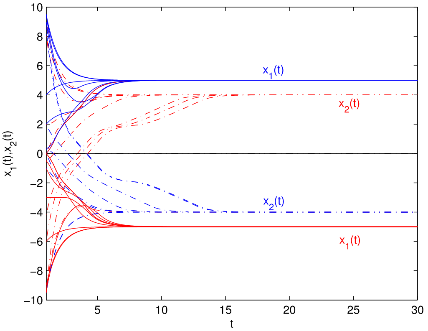
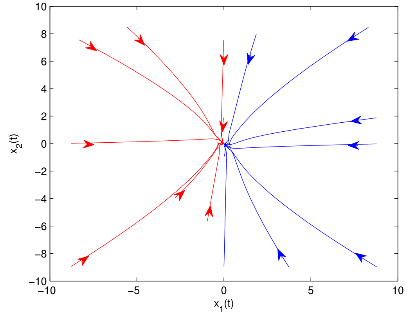
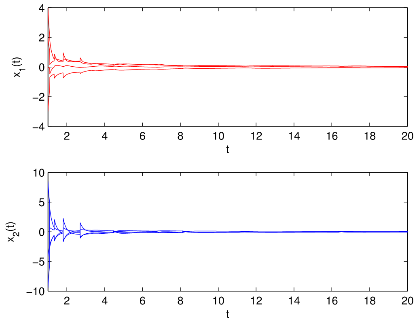
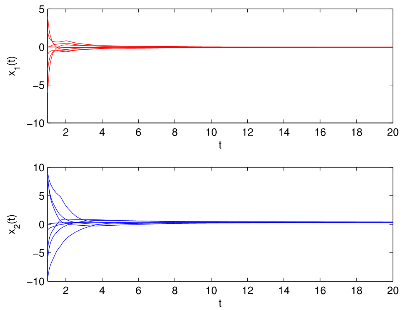
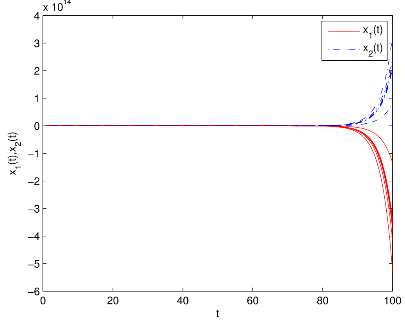
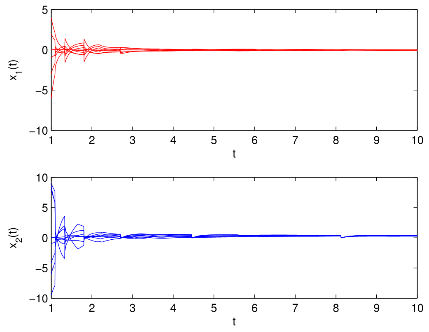
图1 有/无控制器和有/无脉冲作用时双向比例时滞神经网络(BPDNNs)的

相图和时间响应曲线

该工作由爱游戏(ayx)中国官方网站、湖南师范大学、沈阳工业大学、Texas A&M的科研人员合作完成。周立群教授为第一作者，湖南师范大学朱全新教授为通讯作者，爱游戏(ayx)中国官方网站为第一完成单位。该研究获得国家自然科学基金面上项目(11901433、62173139)、天津市自然科学基金面上项目(18JCYBJC85800)和湖南省科技创新计划项目(2021RC4030)的资助。

 论文链接：https://ieeexplore.ieee.org/document/10198676